I’m going to try and explain what a decibel is and why it is used so often. For some reason it seems to confuse a lot of people, especially when used in sound engineering. As it happens the dB is actually really simple once you understand what it is and why it is used.

The first concept you need to get your head around is a dB is nothing more than a ratio, just like saying a 2:1 ratio to mean two apples for every pear, in other words double the amount of apples for every one pear. Instead of linear scaling like this, in the land of dB’s everything is logarithmic. You don’t need to know what that means you just need to know that it’s a ratio. First off a bit of history.
The term decibel was named after Alexander Graham Bell and is in fact based on 1/10th of a unit called a ‘bell’. The bell was originally used in telecommunications but nowadays the bell as a unit is not used and instead the term decibel is used to describe ratios of two numbers based on either 10 or 20 Logarithmic (depending on what is being compared).
The beauty of the dB is it allows you to work with large numbers without the maths becoming cumbersome. Unlike the unit of a ‘volt’ or a ‘watt’ or an ‘ohm’ a dB in itself means nothing until it has a point of reference, in other words for it to have meaning it needs context.
Here’s the most important thing to remember about the dB – there are two basic formulas depending on what you are measuring.
For power measurement (watts etc) you use:
dB = 10 x Log(value 1 / value 2)
For magnitude (voltage/current etc) measurement you use:
dB = 20 x Log(value 1 / value 2)
Value 2 is the reference, so could be ‘1 volt’ or ‘1 watt’ and Value 1 is the value of what you are comparing it to. Therefore the two values are nothing more than the two numbers describing the ratio to each other.
That is pretty much all there is to it!
Let’s take a typical example of an amplifier. If we measure the amount of voltage an amplifier is outputting when it is fed a 1KHz sine wave and find that to be 1 volt we can say that 1 volt is our reference value, in other words Value 2 in our calculation.
If we then change the input frequency to be say, 10KHz and now we find that the output of the amplifier is 0.5 volt we can say that:
0.5 / 1 is the same as down by 0.5 is the same as half is the same as 20xLog(0.5/1)
We use 20Log as Volts are a unit of magnitude. If we punch in 20xLog(0.5/1) to a calculator we see that the answer is -6. This means we now know that:
0.5 / 1 is the same as down by 0.5 is the same as half is the same as -6dB
Here’s some very useful numbers to remember.
For Power (10 Log):
-3dB = 0.5
-10dB = 0.1
For Magnitude (20 Log):
-3dB = 0.707 (a.k.a. ‘half power’)
-6dB = 0.5
-20dB = 0.1
Because dB is a base 10 logarithm, as opposed to natural to base E, we can do calculations of large numbers very easily. Let’s take the ratio of 1000:1 as an example.
We know from the handy list above that for magnitude that -20dB = 0.1, this means that +20dB must = 10. In other words +20dB is the same as saying something is 10 times something else. When calculating our 1000:1 ratio we just need to do some addition based on this value of 20dB. Simply shift the decimal place three times and we get:
1 0 0 0
20dB+20dB+20dB = 60dB
Therefore, when something is 1000 times bigger than something else we can say it is +60dB.
This is of course also works the other way round too. If we want to describe that something is 1000 times smaller than something else (or 0.001) we can say it is -60dB.
If we take the amplifier as an example again but this time we want to calculate the total gain produced by a series of amplifiers we can do that much easier with dB’s. Lets say we have 3 amplifiers in series.
Amp 1 -> Amp 2 -> Amp 3
x2 x10 x31.6 = 632 times the original input signal level
+6dB +20dB +30dB = 56dB
As we see above, one of the great thing about dB’s is that we can simply do addition instead of multiplication and still describe the signal gain.
If our input signal was 1 Volt we can now describe this signal gain as being 56dBV. This is because there are suffixes for dB to describe the reference. In this case ‘V’ is equal to 1Volt meaning anyone can understand what the reference of the ratio actually means. As described above saying ‘dB’ on its own, although it describes the ratio, it doesn’t describe what that ratio is referring to. This is why there are some commonly agreed symbols.
Some common suffixes include:
dBV = 1 Volt
dBm = 1 milliwatt
dBu = a 600 Ω load dissipating 0 dBm
A real world example of this is my Soundcraft mixer (also applies to most mixers) as you see below it has an LED scale of dB values, which on their own would mean nothing, except it tells us that 0dB on the scale is a reference of +4dBu.

In audio, dBm generally refers to impedance of 600Ω, whereas in radio frequency it refers to 50Ω. It is therefore important, even when using common suffixes, to be sure of their meaning in context.
In acoustics, which is where most people are familiar with the use of dB, the reference value is the threshold of human hearing. The measurement of pressure (SPL) uses 20Log as it is a measure of magnitude and the measurement of power (e.g. dB SWL) would use 10Log. SPL uses the threshold of hearing (i.e. the reference value in our calculation) to be that of 20 micropascals. When measuring SPL quite often various weightings are used, such as dB(A) or dB(b) which are meant to reflect the human ear’s response at different frequencies. Although those notations are used the actual reading is still in dB SPL, in other words still uses pascals as the unit for the reference value.
The last important point to make is about log in general. If we take a look at an amplifier’s roll off characteristics, first in a linear graph and then in a log graph, we will see the benefits of using log. You will notice dB on the Y-axis and frequency along X. In case it’s not obvious this would not be an audio amplifier because of the frequency range but the same principle applies.
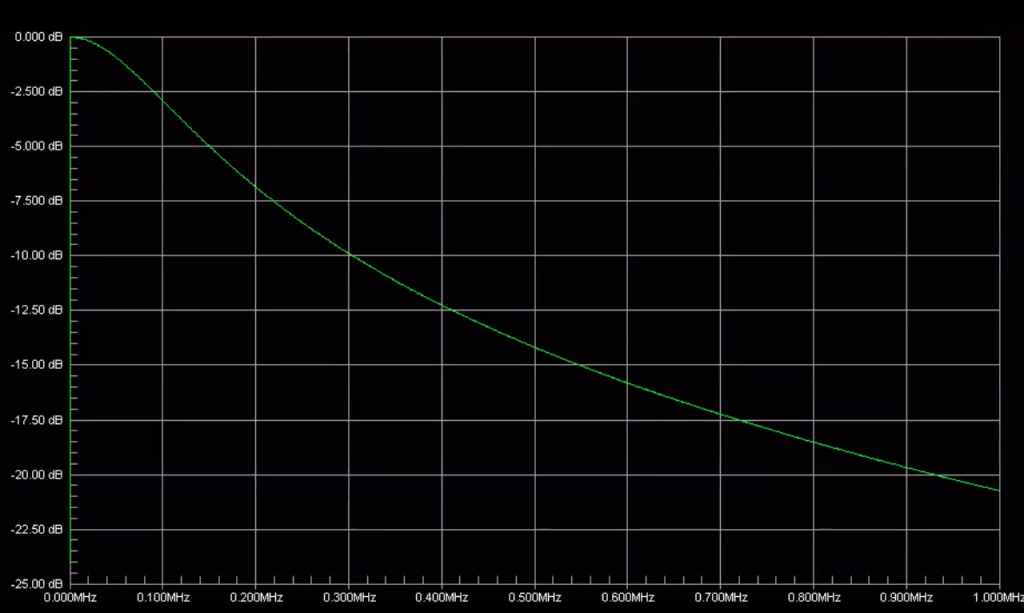
Notice that the roll off is impossible to read. The X axis is linear from 0-1MHz but this means that the narrow bandwidth at the beginning cannot be seen.
Now, instead of using a linear range for frequency we will use a log scale. This time each value for Hz is a ‘decade’ apart. A decade is a factor of 10 between each value – this is also known as an ‘order of magnitude’.
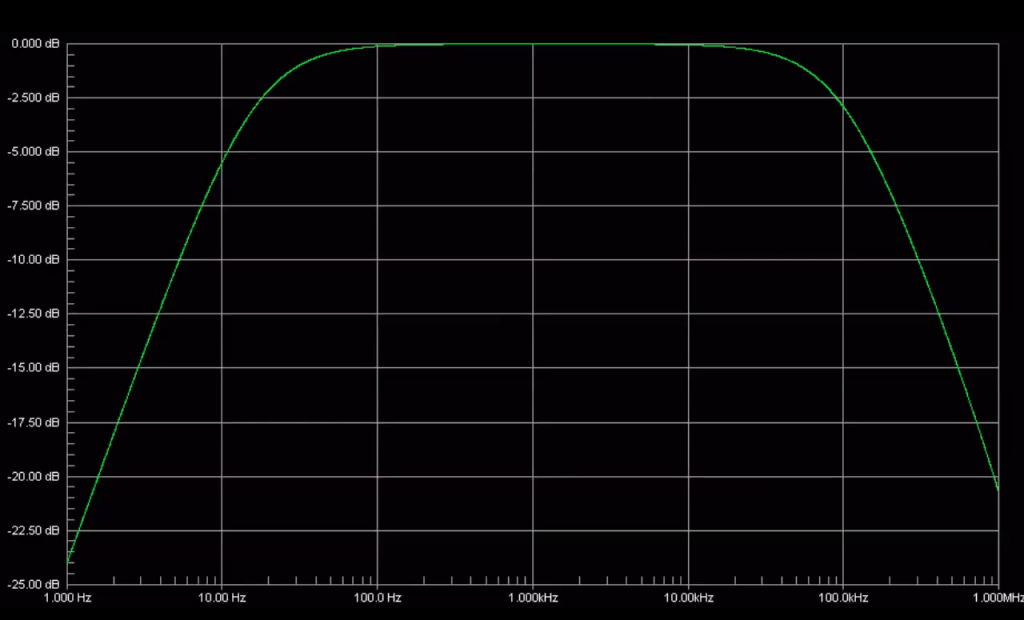
You can now see how much easier this is to read than before and the roll off is now obvious. The graph still shows 0-1MHz but this time, because each value along X is incrementing by a factor of 10, the narrow and wide bandwidths can be read. What we’re seeing here is a typical bell curve which is what almost any roll off graph will look like – providing it’s logarithmic!
I hope this has helped understanding the decibel and why it is used 🙂
Here’s a handy chart reffering to amplifer power and percieved loudness.
| dB Change | Loudness Change | Sound Pressure Change | Power Change | Comments |
|---|---|---|---|---|
| +3 | x 1.23 (+23%) | x 1.4 | x 2 | twice the power |
| +6 | x 1.52 (+52%) | x 2 | x 4 | four times the power, twice the sound pressure |
| +10 | x 2 | x 3.16 | x 10 | 10 x the power, around twice the loudness |
| +20 | x 4 | x 10 | x 100 | 100 x the power, 10 x the sound pressure, around 4 times the loudness |
| +40 | x 16 | x 100 | x 10,000 | loud! |