This article contains information on how to calculate the operating margin of a wireless 802.11 network using a known distance between the two points.

I wrote this quite a while ago and although the throughput of wireless links has dramatically increased the basic theory still applies. Of course we now have 5GHz available, which is very useful for this application. You should be able to substitute ‘f’ for 5000MHz and the maths will still work.

You can now get a 150mbps PTP link over 15km using equipment that costs £160 for both ends – that’s the entire cost of the system (minus a couple of poles and brackets). Crazy value for money when you think about it. The Ubiquiti NSM5 NanoStation is one such example. The Ubiquiti product range is pretty impressive to say the least. The NSM5 seen below is the big brother of the LOCOM5, which at £125 can still do 10km at the same rate and are around half the size.

 

If you are considering an outdoor wireless link, give this article a read so you understand how high above objects you need to mount your shiny new kit!

Step 1 – Convert variable values to required units

Transmitter Power

Covert transmitter power from milliwatts (mW) to Decibel relative units compared to milliwatts (dBm)

This is done using base-10 logarithmic

dBm = 10 x (LOG10 (power in mW))

eg. 30mW = 10 x (LOG10 30) = 14.77 dBm

You will often find manufacturers specify the power output in dBm but incase they don’t be sure to do the above arithmetic.

Required Distance between access points

Convert distance from miles to kilometers

kilometers = 1.609 x (miles)

eg. 1.609 * 9.4 miles = 15.12 km

Step 2 – Calculate required minimum antenna height above highest obstacle

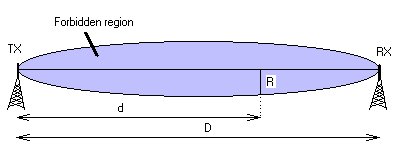
Using the Fresnel ellipsoid we need to calculate the minimum height the antenna must be above the highest object between the two access points.

Height in meters = ((43.3 x SQRT((D x 0.621) / (4 x (f/1000)))) x 0.3048) x 80%

SQRT = Square root

D = distance between points

f = operating frequency (lets assume 2400MHz)

eg. D = 14km and f = 2400mhz

Height = ((43.3 x SQRT((14 x 0.621) / (4 x (2400/1000)))) x 0.3048) x 80% = 10.05m

Point R indicates the radius of the first ellipsoid “forbidden zone” based on the distance ‘d’ from point A to the obstacle.

Calculated using

radius of forbidden zone in meters = 0.6 x SQRT(0.12 x d1 x d2 / (d1+d2))

where d1 = distance from point to obstacle and d2 is total distance between points

eg, d1 = 10 and d2 = 2

0.6 x SQRT(0.12 x 10 x 2 / (10+2)) = 0.26m

For simplicity lets assume there is no object!!!

 Step 3 – Calculate losses

The losses we need to consider are:

• Loss in coax
• Loss in connectors
• Loss in air

REMEMBER: Losses are negative values in reality, but depending how you calculate your final answer, you may keep them as positive integers.

Loss in coax

There are many different coax standards available, we will assume the use of LMR400 coax.

LMR400 has a loss per meter measured in dB of 0.22 (0.22dB/m)

Therefore when calculating coax loss we simply do

loss in dB x length in meters

eg. 0.22 x 3 = 0.66dB

REMEMBER: There are 2 ends to a connection, therefore you must work out losses for both ends!

Loss in connectors

Each physical connector used to connect the antenna to the WLAN card incurs a loss that we must include in our calculation. i.e the plug on either end of the coax, any barrel connectors and lightning protectors you may have.

To calculate the loss caused by connectors

loss in dB = number of connectors x (SQRT(f/1000) x 0.1)

eg. 2 connectors and where f = 2400MHz

2 x (SQRT(2400/1000) x 0.1) = 0.31db

Lightning protectors vary in losses but we’ll assume a general value of 0.5dB

therefore total loss = number of protectors x 0.5

eg. 1 protector

loss in dB = 1 x 0.5 = 0.5dB

REMEMBER: There are 2 ends to a connection, therefore you must work out losses for both ends!

Loss in air (free space)

As you may expect the loss in free space is the greatest loss involved in the total calculation. Many variants affect how much loss is involved, dependant on environmental conditions. For general purpose calculation we’ll use the following formula.

loss in dB = (92.4+(20 x (LOG10(f/1000))))+(20 x (LOG10(D)))

where

f = operating frequency in MHz

D = total distance between points

eg. using 2400mhz over a distance of 13km

loss in dB = (92.4+(20 x (LOG10(2400/1000))))+(20 x (LOG10(13))) = 122.28 dB

Step 4 – Calculate Total Power Radiated

The total radiated power from the transmitting antenna is calculated using the transmitter output in dBm and the gain of the antenna used in dBi.

The maximum gain an antenna in the horizontal plane (specified as dB (Decibels) relative to an isotropic radiator) is the rating in dBi. This is somewhat misleading as it is the maximum theoretical gain around a virtual sphere which can never exist in real life, but does provide us with a rating to use in our approximate calculations. A dish shaped antenna, such as a parabolic mesh, radiates in a circular polarization pattern and not direct horizontal or vertical as with traditional antenna and normally have a higher gain, the more directional an antenna is, the higher the gain. The disadvantage of a highly directive antenna is they have have to be aligned with greater precision. If the gain of an antenna is given in dBd (gain relative to a dipole) then 2.14 is added to the value to give the gain in dBi.  

Total radiated power = transmitter power + antenna gain – losses in coax and connectors

When we calculate total radiated power we have to make sure it falls within FCC rules which state no more than 20dBm from the antenna. This is known as EIRP and your equipment must not transmit above this threshold in the UK.

e.g. Transmitter Power = 15dBm

    Antenna Gain = 20dBi (typical 1m parabolic mesh)

     Losses in coax and connectors = 0.91dB

Radiated power = 15 + 20 – 0.97 = 34.03 dBm

As you see in this example it would illegal to run this system in the UK

I’ve neglected to mention a very important factor in the calculation of total radiated power from the antenna. This factor is the Standing Wave Radio (SWR or VSWR) of the transmitting setup. 

SWR is the ratio of the maximum RF (radio frequency) voltage to the minimum RF voltage along the line (or current). This ratio is calculated by comparing the total transmitted power from the transmitter to the total reflected power back to the transmitter. To achieve an SWR of 1:1 the entire feed from the transmitter should be of matching impedance to the antenna, therefore creating a balanced line and the load (ie the antenna) having no inductance or capacitance for an ideally efficient transmission. If the impedance of the antenna is not the same as the transmission line the antenna does not transmit all of the RF power being transmitted into it (this is the forward power or FPWR) and therefore some of the RF power is sent back down the line into the transmitter, this is the reflected power or RPWR. When this happens it creates patterns of voltage maximas (also known as loops) and minimas (also known as nodes) which we use to calculate the ratio. In extreme cases these can produces thousands of volts at various points along the transmission line. If we think of this theoretically we can say the potential maximum SWR is infinity but in reality this is not the case due to the resistance of the transmission line. By using the correct coax, connectors and ensuring a good solid connection between components you should be able to retain an SWR of 1:1 or there abouts. Unfortunately the equipment required to test SWR at 2.4Ghz isn’t cheap and most people don’t bother testing this. 

Here is an example of an extreme situation whereby the reflected power is half of the transmitted power. To confuse matters this formula requires the input of milliwatts (mW) (or watts (W)) instead of dBm as calculated in the first section.

F = 1 + ((sqrt)RPWR / FPWR)
R = 1 –  ((sqrt)RPWR / FPWR)

SWR =      ((F/R) x 100 x 0.5)
100

E.g. Where:
FPWR = 10
RPWR = 5

F = 1 + ((sqrt)5 /10)     = 1.707
R = 1  – ((sqrt)5/10)     = 0.293

SWR =     ((1.707 / 0.293) x 100 + 0.5)        = 5.831 
                                100

= an SWR of 1:5.831 or  1 : 6

As a general rule you should not operate a transmitter if the SWR is greater than 1:2
After all those long calculations you’re probably wondering what you’re meant to do with this ratio! Well… All you really need to know is the reflected power because you take this figure and apply it to:

actual transmitted power = total forward power – total reflected power

Once you know your actual power you apply it to the conversion to dBm in section 1 and use it for the rest of the calculations.

Step 5 – Calculate the received signal

Radio receivers used in wireless data communications have a minimum threshold that must be met to attain the full potential speed, i.e. bit rate. If the received signal falls below this threshold performance will be serious degraded, this includes maximum throughput and latency. The faster the connection, the higher the threshold. The card I am using is a D-Link DWL-510 and has the following thresholds at 8% packet error rate:

11mbps < -80dBm

5.5mbps < -80dBm

2mbps < -87dBm

1mbps < -90dBm

To make matters worse receivers have a Signal to Noise Ratio (SNR) which is an indication to the requirement of the strength of the useful signal being ‘pulled in’ by the antenna, the useless signal is known as noise and is filtered out. If the usefull signal is greater than the noise then we have a positive SNR value. If the noise drowns out the signal then the link won’t be achieved.

SNR  = 10 x Log10 (Signal Power / Noise Power )

[If the noise level is very low then the system will be limited more by the receiver sensitivity than by the S/N ratio. If the noise level is high then it will be the Signal/Noise ratio that will count to achieve a given data rate. If the noise level is high we will need more received power. In normal conditions without any other WLAN on the frequency and without industrial noise the noise level will be around -100dBm. For example to achieve a 11 Mbps data rate with an Orinoco 802.11b card we would need a received power 16dB higher (S/N ratio) so a level of -100+16=-84 dBm but in fact the minimum receiver sensitivity is at -82 dBm…higher than -84. It means in that case the minimum receiver sensitivity is the limiting factor for the system.] extract from another site

received signal = transmit power – transmitter cable and connector loss + transmit antenna gain – receiver cable and connector loss + received antenna gain – loss in free space

eg. transmit power = 15dBm

transmitter cable and connector loss = 0.31dB

transmit antenna gain = 20dBi

receiver cable and connector loss = 0.91dB

received antenna gain = 20dbi

loss in free space = 122.28dB

received signal = 15 – 0.31 + 20 – 0.91 + 20 – 122.28 = -68.5dB

You may wonder why this is a negative number? The reason is quite simple, there is no physical connection between the transmitting and receiving antenna, therefore the receiver’s sensitivity is rated as a negative. Next we will work out the margin of the connection to see if this setup will work.

Step 6 – Work out the Operating Margin

A WLAN card will always have a sensitivity clearly marked in the specification. This number will be negative and is used to compare with the received signal.

eg. Taking the figures from above for the D-Link DWL-510 we can see that @ 11mbps it has a sensitivity of -80dBm

To work out the margin we do…

margin = received signal – sensitivity

eg.

margin = -68.5 – (-87) = 18.5dB

The required margin is in the region of 10dB. As we see in this situation our link would work, if it falls below 10dB we can expect a drop in performance. In theory, if we reached 0dB for 11mbps the speed would decrease according to the sensitivity figures stated above, in real life it happens before these values are reached.